Proof Blocks ▸ Research
Implementation
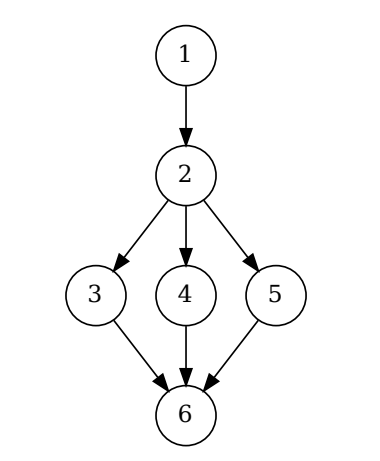
When constructing a problem, the instructor specifies the dependency graph of the lines of the proof, so that any correct arrangement of the lines can receive full credit. The grader will accept any topological sort of the dependency graph as a correct proof.Proof Blocks: Autogradeable Scaffolding Activities for Learning to Write Proofs by Seth Poulsen, Mahesh Viswanathan, Geoffrey L. Herman, and Matthew West. Innovation and Technology in Computer Science Education 2022
Efficient Partial Credit Grading of Proof Blocks Problems by Seth Poulsen, Shubhang Kulkarni, Geoffrey L. Herman, and Matthew West. International Conference on Artificial Intelligence in Education 2023
Proof Blocks Problems as Exam Questions
We used Proof Blocks in a discrete math course with hundreds of students. Our psychometric analysis showed that Proof Blocks problems gave substantial information about student knowledge while being easier than written proofs. Student surveys showed that students felt that Proof Blocks were easy to use and gave them an authentic proof-writing experience.Evaluating Proof Blocks Problems as Exam Questions by Seth Poulsen, Mahesh Viswanathan, Geoffrey L. Herman, and Matthew West. Honorable Mention for Best Paper, International Computing Education Research conference 2021

Proof Blocks for Learning
Research has shown that in some situations, Parsons Problems can help students to learn as much as writing code from scratch, but in a shorter amount of time. Similarly, Proof Blocks problems help students learn to write proofs more quickly than writing proofs from scratch alone.Efficiency of Learning from Proof Blocks Versus Writing Proofs by Seth Poulsen, Yael Gertner, Benjamin Cosman, Matthew West, and Geoffrey L. Herman. SIGCSE Technical Symposium 2023

Problem Autogeneration
We're working on generating problems that look like the informal, natural language proofs that students are used to, but generated from a formal proof assistant such as Coq. Having a underlying formal representation of the problem will allow us to do implement novel technologies such as autograding proof problems that include fill-in-the blank boxes, randomly generating new proof problems for students, and more.Autogenerating Natural Language Proofs for Proof Education by Seth Poulsen, Matthew West, and Talia Ringer. The Coq Workshop 2022